Thinking Machines
Machine learning is used everywhere, it finds its application in a number of diverse fields ranging from targeted advertisements to disease diagnosis to Crystallography.
So what is Machine Learning? And why is it so successful? In 1959, Machine Learning was defined by Arthur Samuel as the “Field of study that gives computers the ability to learn without being explicitly programmed”. Simply put, machine learning algorithms give computers the ability to learn from data.
These algorithms take in data and try to figure out patterns within them, once a pattern is discovered it is then used for prediction when new data comes along. Let’s study a simple situation where machine learning can be used. Suppose, we would like to figure a way out to predict the price of a house given its area. The only information we have is a bunch of prices of houses and their corresponding areas
| Area | Price |
|---|---|
| 1000 | 18000 |
| 2200 | 23000 |
| 2500 | 49500 |
| 3100 | 51500 |
| 4500 | 77500 |
| 5200 | 64000 |
| 6100 | 91500 |
| 7400 | 124000 |
This data in itself does not tell us much, lets try to plot this data and see what we get
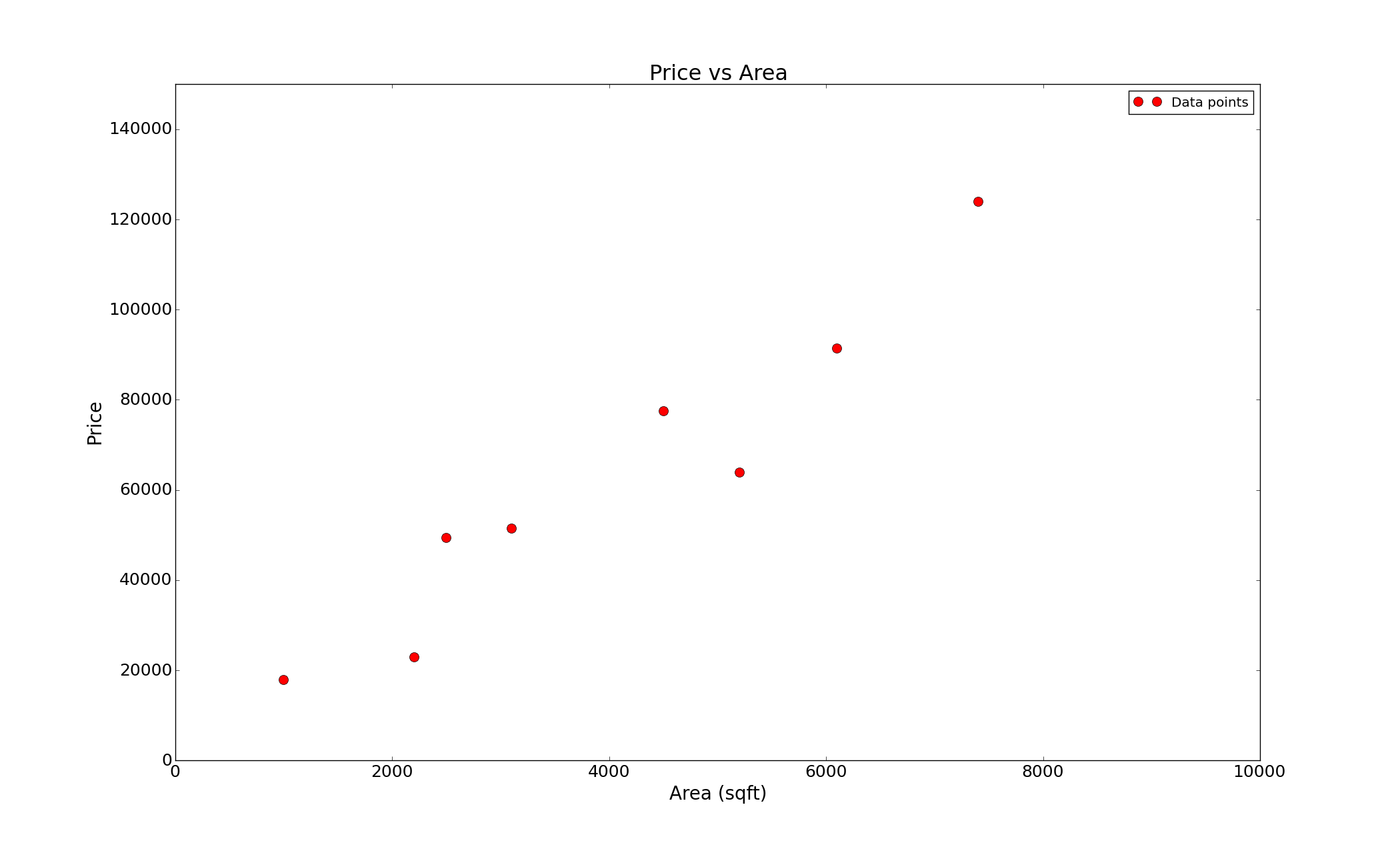
Looking at the plot one can, with reasonable certainty, conclude that the price depends linearly on the data, or in math speak it follows this form
\[P = wA + t\]This line is what we call a regression line. Here \(P\) is the price, \(A\) is the area and \(w\) and \(t\) are two constants.
But what is the exact dependence? What are the exact values of \(w\) and \(t\)? is the price twice the area? ten times the area? or 13.278 times the area? Before we try to answer those questions, we must have a way to measure how well the regression line describes the data. To do this we define an error function of the following form
Where \(n\) is the number of data points, since we have eight data points, \(n = 8\) in this case. If our predictions are perfect then this function will be zero, but if they are not then this function will take a value which is directly proportional to how bad our predictions are. The right values of \(w\) and \(t\) are the ones at which this function will assume its lowest value. One can minimize this function in a number of ways, and for this rather simple problem there exists an exact formulae that give the values of \(w\) and \(t\). Using them, the values we get are \(w = 15.57\) and \(t = 83.31\). Plotting the regression line with the data we get
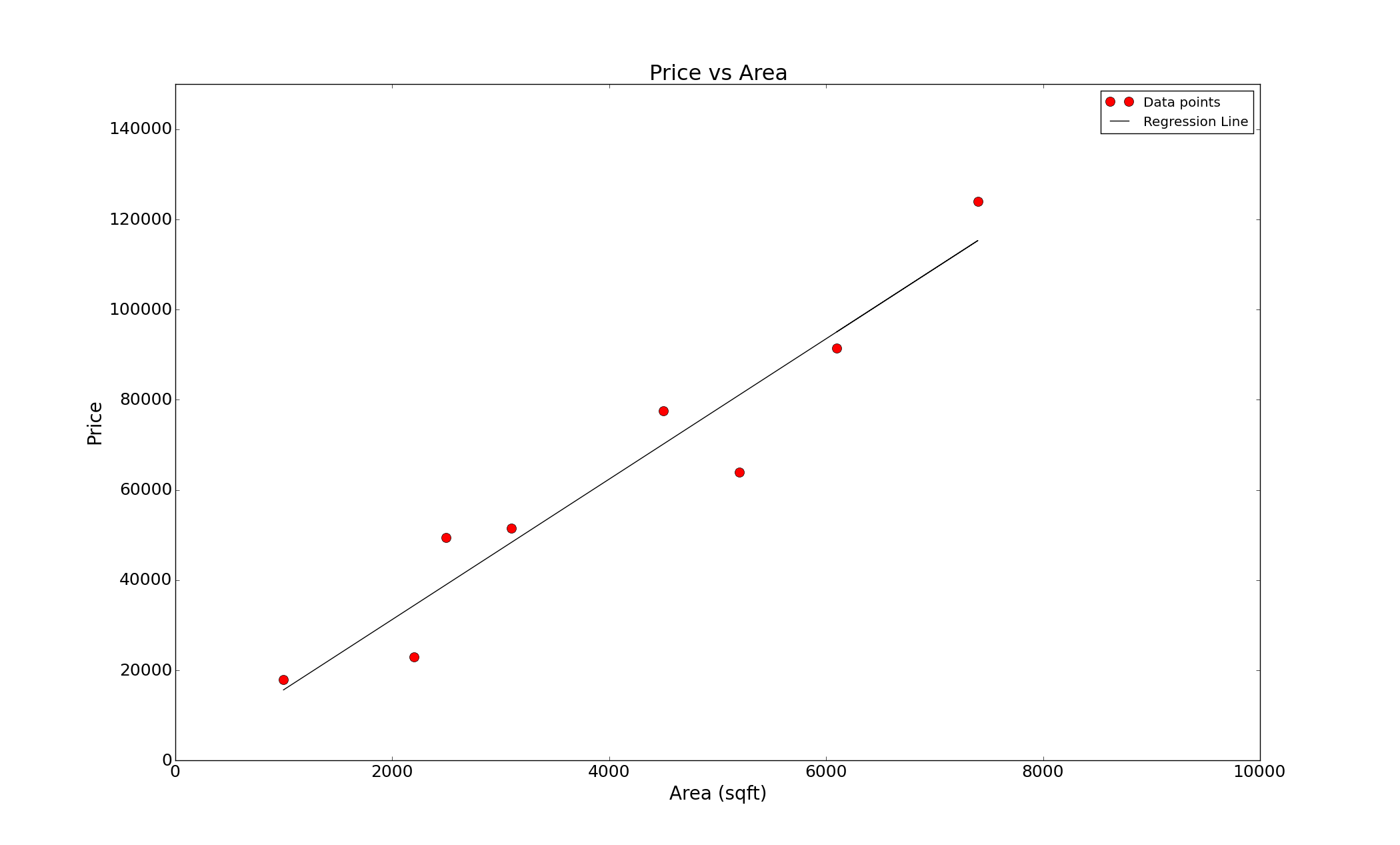
The algorithm we just used is called Linear Regression. Linear Regression is the simplest machine learning algorithm there is, yet it captures the essence of what most machine learning algorithms are i.e we have a cost function that we minimize using a model (in this case it was a straight line), once the cost is minimized we can use this model to predict values. The problem too is very simplistic. Our model just uses one input i.e the area to predict the price, however, more often than not the price depends on more things such as location, number of rooms, materials used and so on. In such cases, instead of passing a number as input to the model we pass in a vector of inputs ([area, location, number of rooms …]) of length \(n\), where \(n\) is the number of parameters the output depends on or the number of “features”. Similarly, the output of the model can also be a vector of some length depending on the problem. Further, we knew (or rather, guessed) a priory what are the features the price depends on and that the dependence was linear. In most problems we do not have such luxuries, we have no intuition as to what the right features are and how the output depends on them. However, a number machine learning algorithms (like neural networks) are able to learn the features and functional dependencies automatically! That’s like an algorithm just looking at the price of the houses and their features and coming to the conclusion that the price probably depends on the area of the house, it does not depend on the color of its door and that it depends on the area linearly. Now that is powerful.
In conclusion, machine learning has proven to be very useful to solve a wide variety of problems in a number of different fields. More recently, it has been used extensively in developing machines capable of human-like cognitive abilities. Convolutional Neural Networks, for example, have been had a great run in computer vision problems. Given raw pixels from a photograph, not only is this algorithm able to predict correctly what is in the picture but it does so by learning along the way what the important features of the picture are. Recurrent neural networks are similarly showing great promise in the field of Natural Language Processing, an area of computer science that deals with getting computers to understand human languages. Recent advancements in reinforcement learning too have shown a similar trend. Using deep neural networks, researchers at Google Deepmind have given computers the ability to reach human level cognition and control in simple Atari game environments. Such feats have also led to the hysteria of developing artificial intelligence that might turn on us. However, as Andrew Ng said “that’s like worrying about overpopulation on Mars, we haven’t even landed there yet!”. Current machine learning algorithms are nowhere close to human cognitive ability in unrestricted environments, and it would take us some time to get there. However, it does seem possible and there is no reason to believe that we can’t develop them, probably in about 100 years we would wonder how we ever lived in a world without artificial intelligence.